Linear Regression
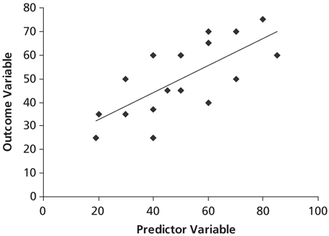
When we want to compare two things we create a graph so we can visually see our results or data. When correlating this data, the data plots randomly unable to give us a line that we can use to predict larger numbers that our graph would show if it continued on. We create a line of best fit that represents all of the plotted data that can run through some plots or zero plots. This line of bet fit can be used to predict any number of your variable you want to compare and you can expect this to be true. In other words, we create a general line that will sum up our graph that can be used to predict and expect any two numbers concerning these two variables on this graph.
Standard Formulas

We all know in math when the teacher gives you a formula, it is generic which means it contains variables which you will fill in to get your answer. With these general formulas, one can expect to get the right answer because if the formula is calculated correctly, you should be able to find your answer.
For example: Say you want to find the perimeter of a square. Mathematicians were able to come up with a generic formula that would stay true for any square. If the Perimeter of a Square formula is P=4s, P equaling the perimeter and s equaling the length of one side and s is given to equal 7 units we can sub in 7 for S and simply multiply to find P. We are left with P=4 x 7 therefore P=28 units
For example: Say you want to find the perimeter of a square. Mathematicians were able to come up with a generic formula that would stay true for any square. If the Perimeter of a Square formula is P=4s, P equaling the perimeter and s equaling the length of one side and s is given to equal 7 units we can sub in 7 for S and simply multiply to find P. We are left with P=4 x 7 therefore P=28 units
Sequences
A sequence is a set of numbers that have a common trend to get from one number to the next. There are two types of sequences: arithmetic and geometric sequences. In arithmetic sequences, you must add a certain number to get to the next number- this number can be negative or positive and it is called the common difference. In geometric sequences, you multiply to proceed throughout the sequences and you can multiply by a positive, negative, and even a fraction- this is called the common ratio. These common "numbers" that are being added or multiplied can lead you to expect any number in the sequence.
